Introducción.
- La radiación térmica y el efecto fotoeléctrico se explicaban muchos fenómenos de radiaciones y emisiones pero no había explicación para los espectros atómicos.

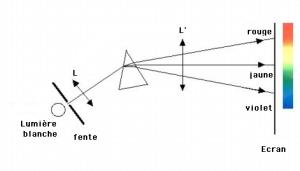

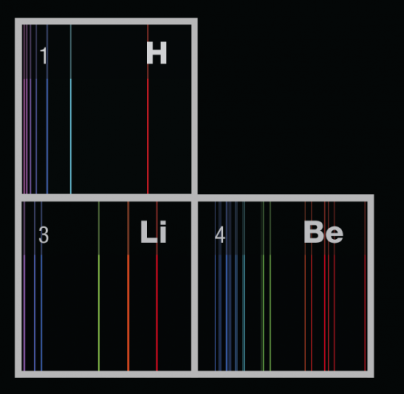
Puedes observa una simulación de los espectros de emisión de los elementos de la tabla periódica pinchando aquí.
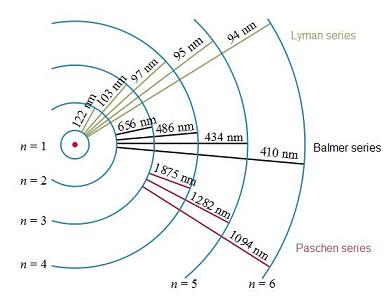
Obra publicada con Licencia Creative Commons Reconocimiento Compartir igual 4.0