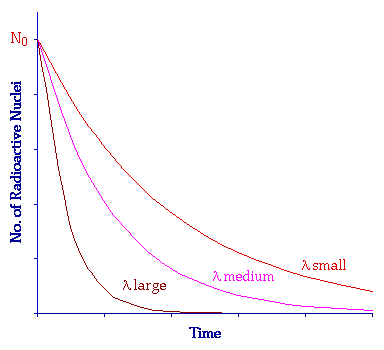
Actividad radiactiva.
Actividad radiactiva: es la cantidad de núclidos que se desintegran por unidad de tiempo.
- En la práctica es la cantidad de núclidos que se van transformando en otra sustancia.
- Depende de la naturaleza de la sustancia que se refleja en forma de constante, $\lambda$, llamada constante de desintegración. Se mide en $s^{-1}$.
- Indica la probabilidad de que un núcleo se desintegre en 1s.
- Cada sustancia tiene su propia $\lambda$.
- Así pues la actividad queda definida por: $$ A(t) = - \frac{dN}{dt} = \lambda \cdot N $$.
- Se mide en desintegraciones/s o también llamados bequerelio. 1Bq = 1 desintegración /s.
- Otra unidad es el Curie $\rightarrow 1Ci = 3,7 \cdot 10 ^{10} Bq$